近日，我院2023级博士生周佳与颜谨教授合作的研究成果Counterexamples to the linkage conjecture for tournaments在组合数学与图论领域国际顶级期刊Journal of Combinatorial Theory, Series B正式发表。该成果通过构造反例，推翻了有向图理论中的备受关注的前沿热点猜想，产生了广泛学术影响，并荣获 2025 山东省研究生创新成果奖。

连通性（connectivity）与连接性（linkage）是图论与组合数学中的基础核心概念，广泛应用于网络结构分析、信息传输与算法设计等领域。图与有向图中“高连通性是否必然蕴含连接性”这一课题备受学界瞩目，英国皇家学会院士（兼匈牙利科学院院士）Bollobás、丹麦皇家科学院院士 Thomassen，以及英国皇家学会院士 Kühn 等国际顶尖专家均曾深入研究并取得相关成果。

2015年，伦敦大学Pokrovskiy 提出猜想：若竞赛图的连通度达到 2k 并满足一定的最小半度条件，则必然是 k-连接的。然而，该猜想在相当长时间内未能被证伪或完全解决。

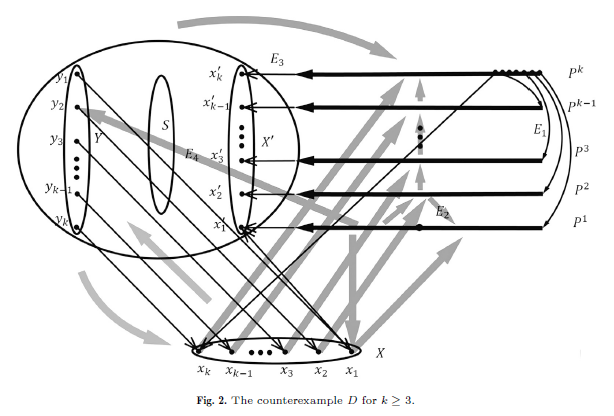
针对上述关键问题，周佳通过精巧的构造方法，首次系统构造出一类具有任意大最小半度的 2k-连通竞赛图，但其并非 k-连接，从而彻底否定了该猜想。同时，该结果也对 牛津大学Girão 等人在Combinatorica中提出更强的热点问题给出了明确的否定性回答，该结果揭示，在竞赛图中，仅依赖 2k-连通性，即使附加很强的度条件，仍不足以保证 k-连接性。这一结论打破了学界的固有认知。

该研究不仅在理论层面厘清了竞赛图中连通性与连接性之间的内在联系，而且为后续探索“最优连通性条件”“最小度阈值”以及更一般有向图的连接性质提供了重要参考框架，对组合结构理论的发展具有基础性意义。

该研究由周佳为第一作者、颜谨教授为通讯作者共同完成。在国家自然科学基金的资助下，这项工作因其突出的原创性与学术价值，荣获 2025 山东省研究生创新成果奖。

一、从“经典问题”走向前沿突破

回溯这项成果的起点，源于一次极其朴素、甚至略显偶然的学术经历。

研一入学之初，为了帮学生们找准方向，颜谨教授特设讨论课，带着学生从经典专著学起。在一次章节分工中，周佳负责整理和讲解 “连接性” 相关内容，这也让她第一次真正领略到连接性问题的魅力 ——她惊叹于其证明思路的巧妙，更着迷于这一纯理论问题背后极其直观的现实原型：就像在一个庞大的网络中，无论你如何挑选k个发送端和k个接收端，也无论你如何规定它们之间的“配对关系”，这个网络都能精准地找出k条“互不干扰”的专属通道，让每一对用户都能按指定的路线“点对点”直达。这种源于现实、归于逻辑的特质，一下子吸引住了她，也正是在这一刻，她与自己的 “真命课题” 不期而遇。

通过查阅资料，周佳了解到：与无向图领域已成熟的理论体系相比，有向图的相关理论发展明显滞后。学界一直期待能在竞赛图这类特殊有向图中，建立起与之匹配的结论，并将其发展为有向图研究中强有力的理论工具。2015年，学者Pokrovskiy基于前人工作提出一项大胆猜想：只要竞赛图具备足够高的连通度与最小半度，便必然具有k-连接性。该猜想因与无向图理论高度呼应，因此被广泛认为是成立的。

周佳的探索之路，便从对这一经典课题的思考开始。

二、在“所有人都相信”的地方反向思考

研究初期，周佳也曾沿着前人的足迹，试图攻克这一猜想。然而，反复的碰壁让她逐渐产生了一个大胆的念头：问题的症结或许不在方法层面，而在于方向本身。面对这一被学界广泛认可的理论，她虽有过短暂的犹豫，但最终还是鼓起勇气向颜谨教授提出了质疑：“老师，会不会这个猜想本身就不成立？”

“既然你有这个想法，那就大胆去试。” 颜谨教授的这句鼓励，成为了周佳研究生涯的关键转折点。她毅然调转思考方向，从 “证明者” 变身 “反驳者”，踏上了构造反例的艰难征程。

但构造反例的难点在于：这个反例必须同时满足所有看似“足够强”的条件，却依然不具备目标性质。“我们的目标是 k 条不交路径，那我就要构造一种路径阻断机制。”在论文中，她精心构造了一类竞赛图：这类图虽然在连通度和最小半度数上都达到了 “足够大” 的标准，甚至最小半度可以随着图规模无限增大，但却无论如何都无法找到 k 条按指定端点连接的互不相交路径。这一构造直接否定了“2k 连通 + 高半度数 ⇒ k-连接”的猜想，且进一步研究表明，2k+1连通恰好是一个不可再降低的阈值。这一结果不仅反驳了 Pokrovskiy 猜想，也对 Girão 等人在组合数学与图论领域公认的顶级期刊Combinatorica的问题给出了否定回答。

周佳坦言到：事实上，我们不仅希望推翻猜想，更希望构造一种普适的路径阻断结构，让即便在高连通、高密度、高强度条件下，指定端点间的一一对应路径依然无法存在。

三、师者如光，微以致远

回顾全程，周佳多次强调导师颜谨教授的悉心指导与一路支持。在她看来，导师的引领不仅体现在具体论证的推敲上，更在于为她指明了清晰而长远的研究方向。

从研一的基础训练到逐步逼近核心问题，颜老师始终以分阶段、可执行的方式帮助她拆解目标。每完成一个局部构造，师生二人便深入探讨、校准方向。正是颜老师的这份循序渐进的悉心指导，使她在高强度的理论探索中始终保持着清晰的路径感。而在那些充满不确定性的时刻，老师一句“你肯定能做出来”的鼓励，成为她坚持下去的精神支撑。在颜老师学术严谨与心理信任的双重加持下，她最终跨越瓶颈，实现突破。

此外，周佳特别提到，山大数学学院系统且多元的培养体系，如同一个丰富的知识生态系统，为她的科研之路注入了多维养分：王光辉老师的《随机图》课程严谨细致且兼具前沿性，不仅夯实了她的理论根基，更教会她在科研与写作中追求极致的逻辑缜密与细节完美；吴建良老师的《算法分析与设计》，则以幽默风趣的授课方式，让她在轻松的氛围里吃透复杂知识点，真正体会到 “快乐学习” 的乐趣与高效；而吴吉昌老师的《最优化理论与应用》与颜谨老师的《图论及其应用》，通过讨论式与翻转课堂的模式，着重锤炼了她独立思考、口头表达及主动探索的学术素养。

四、求真务实，在积累中等待突破

在周佳看来，理论数学研究的最大挑战，并非技巧本身，而是长期的孤独与不确定性。

“如果没有热爱，是很难坚持下来的。”她强调，“另外，我很看重求真务实。对外要求证，对内要认识自己的兴趣、能力和不足，然后脚踏实地地去做。”

在具体方法上，她养成了高度自律的科研习惯：持续追踪最新文献、系统做笔记、在阅读后讲给自己听，用复述的方式加深理解；将长篇证明整理为清晰的逻辑结构，确保每一个细节都经得起推敲。

五、寄语后学，砥砺前行

回顾在数学学院的求学时光，周佳认为自己最大的变化是“更坚韧了，也更有勇气了”。讨论式、翻转课堂式的教学氛围，让她在一次次表达与思辨中不断成长；学院严谨而开放的学术环境，使她学会在尊重前人成果的同时，也敢于提出质疑。

谈及对师弟师妹的寄语，她这样说：“迷茫和焦虑都是常见的状态。等你拨开云雾的时候，会感谢这段经历。人生处处是斗转，左转三次，便是右转。”

在不被怀疑的地方提出怀疑，在长期积累中实现突破。周佳用她的科研历程诠释了何为“求真务实”，也为更多走在学术之路上的年轻人，点亮了一盏敢于质疑、踏实前行的灯。